But what about the last one?  Is Earth really a ball?  Of course it is, but how do we know?  From where we stand it certainly doesn’t look that way.  Obviously we could just visit http://www.nasa.gov and download a few satellite photographs.  Or ask any astronaut, or pilot who’s travelled to the edge of space – they’ve seen the curvature of the Earth with their own eyes.  The thing is, though, our grandparents already knew that the Earth was round long before we had space travel.  How?

Well, a number of great expeditions were made in the 18th and 19th centuries in which brave men armed with theodolites and other surveying equipment mapped out large areas extremely precisely.  If you look at their data you find all manner of triangles appearing whose angles add up to more than 180 degrees.  Now anybody with high school geometry knows that the angles of a triangle on a flat surface always add up to exactly 180 degrees, so clearly the surveyors of old either took sloppy measurements, or the surface of the Earth curves (spherical geometry tells us that the interior angles of a triangle on a curved surface always add up to more than 180 degrees).  Of course, there were hundreds of such surveys and their numbers all agreed (to a reasonable degree, at least), which forces us to conclude that the Earth’s surface does curve, and since the curvature is almost the same everywhere, the Earth must be a giant ball.  But the surveyors weren’t surprised by this discovery.  In fact, they were already compensating for it, as it was common knowledge that the Earth was round.  So how did they know?

Most people would be surprised to learn that educated folk have known the true shape of the world since before the birth of Christ!  But how?  It all starts with Lunar Eclipses.  To a thoughtful observer, it’s easy to work out what’s going on with a lunar eclipse.  If you plot the paths of the Moon and the Sun through the sky, you’ll notice that whenever they’re at their furthest points from each other in the sky (About once a month), you get a full moon.  From the shape of the phases of the moon, it’s pretty obvious that the Moon is round and that it’s being lit up by the Sun, and the different phases are directly connected to their relative positions.  The Sun and the Moon each travel their own paths, but occasionally they line up almost exactly opposite each other in the sky and when this happens you also happen to get a Lunar Eclipse.  Now the geometry of this alignment means that the Earth must be exactly between the Sun and the Moon, so it’s fairly obvious that what we’re seeing is the Earth’s shadow covering up the Moon.  This much was pretty well-known even in ancient times, but the important detail noticed by ancient astronomers was that the shape of the shadow as it crosses the moon was always round.  Now you could try to explain this by saying that the Earth is shaped like a disk, but no matter what angle the Sun-Moon line passes through Earth, the shadow was always the same shape.  To a student of geometry (and the Greeks knew all about geometry) there was only one possible explanation:  The Earth must be spherical.  This posed all sorts of problems, like how come people don’t fall off the sides and the bottom, and led to a bunch of clever-but-wrong theories until Isaac Newton saved the day with his Theory of Universal Gravitation.

But they went better than merely knowing the shape:  They knew the size too, and quite accurately.  How?  Roughly two hundred and fifty years before Christ, a man known as Eratosthenes of Cyrene (These days it’s called Libya, in North Africa) lived in the Egyptian city of Alexandria where he held the position of Librarian at the famous library.  Eratosthenes was first and foremost a mathematician, but managed to gain renown for his contributions to philosophy, poetry, astronomy and music.  He also invented the field of geography, presumably in his spare time.

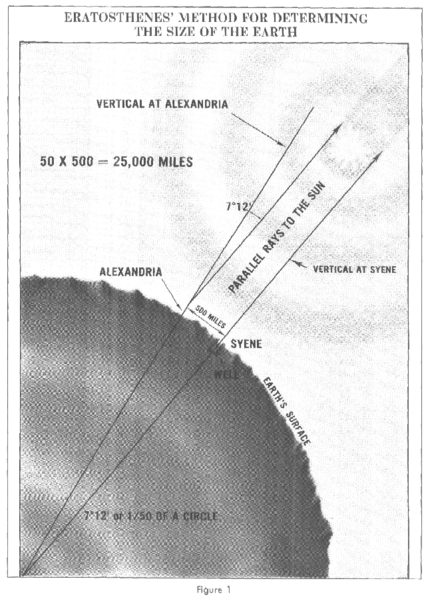The city of Syene (modern-day Aswan, in Egypt) happens to lie almost exactly on the Tropic of Cancer meaning that at noon on the day of the June Solstice, the Sun shines exactly overhead.  If a citizen of Syene were to plant a perfectly vertical stick in the ground at that time, it would cast no shadow whatsoever.  When Eratosthenes heard about this trick he was intrigued, as it did not work in Alexandria – there would always be a shadow, no matter what time or date he tried.  Since he already knew the Earth to be spherical, it was obvious to him that the Sun’s light must strike Syene at a different angle to Alexandria.  It occurred to him that if he knew this angle (Very simple to calculate by measuring the length of the shadow and applying basic trigonometry), and the distance between the two cities, then it would be quite simple to calculate the circumference of the Earth.  He did this, and found a figure of 250,000 stadia.  Unfortunately nobody is entirely sure how accurate he was, since the stadium was not a standard length – depending on which sources you consult, it is somewhere between 155 and 170 meters.  Still, even with this large margin of error, his results were within a few percent of the true figure and remained the most accurate available for a very long time.

Of course, there are plenty of other demonstrations we can offer to convince the Flat-Earther that our world is round, and any school-child can list at least a few.  Everything from the way ships vanish over the horizon to the fact that those ships can sail all the way around the world, but these only become obvious when you already know the world is round.  And for that knowledge we can thank the ancient Greeks and their careful deductive logic.

---

Comments?  Questions?  Why not mail me at [email protected]